
Hola de nuevo a todos. A petición de un amiguete, hoy os voy a dejar un sencillo tutorial sobre punteros. Para ello hay que tener unos conocimiento básicos, muy básicos, de programación. Por lo que aquellos que no los tengan deberán hacer un esfuerzo extra, o esperar al siguiente artículo, que espero que sea en no mucho tiempo.
El texto se puede tomar para prácticamente cualquier lenguaje de programación que soporte punteros, pero los ejemplos los mostraré haciendo uso del
Lenguaje C.
Primero hablaremos de cómo un ordenador maneja los datos. Para un ordenador, datos pueden ser una letra, un número, una fotografía, una película o la discografía de nuestro grupo favorito en MP3.
La Memoria RAM
Los datos se pueden almacenar en muchos soportes: en CD, DVD, disco duro, disquete, una unidad USB, etc. pero cuando trabaja sobre ellos siempre necesita almacenarlos en la
memoria RAM.
La memoria RAM se divide en páginas y/o segmentos, y estos a su vez en palabras, que se componen de bytes, que son un conjunto de 8 bits (un bit es un 0 o un 1). Para esta introducción a los punteros nos centraremos en las palabras, que es la unidad base de memoria del ordenador. El tamaño de la palabra se mide en bytes o bits, y para complicación nuestra varía según el modelo de ordenador, aunque lo normal es encontrar ordenadores que trabajan sobre palabras de 32 bits (4 bytes) o 64 bits (8 bytes). En cualquier caso no nos pararemos a complicarnos con esto. Para nosotros una palabra es una palabra y punto.
Cada palabra es como un pequeño casillero donde se pueden meter datos. ¿Cuantos datos se pueden meter en una palabra? Pues no muchos la verdad, ya que es la unidad base con la que trabaja el ordenador. En una palabra generalmente cabe un número o un carácter ortográficos. De esta forma una frase como "Hola que tal?" necesitará 13 casillas, una por cada carácter, incluyendo los espacios en blanco. Un número grande o con decimales podría ocupar más de una casilla, y una película o una canción ocupan muchas, muchas, muchas casillas.
Variables
En un lenguaje de programación, se suele asignar un nombre y un tipo a una casilla o conjunto de ellas, para luego en el propio lenguaje poder utilizar los datos de esa casilla en operaciones o sustituirlos por otros sin perder a la casilla de vista en ningún momento. A esto se le denomina una variable, y se puede definir así:
char letra = 'A';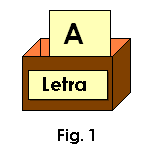
La palabra
char indica el tipo de contenido de la variable (tipo carácter) y la palabra
letra el nombre que le asignamos a la variable para poder hacerle referencia más tarde. Además, en la misma línea le asignamos un contenido inicial, la letra A, pero podríamos a haber creado una variable sin asignarle ningún contenido inicial (en la práctica no es recomendable). De esta forma tenemos una casilla con el nombre
letra y de contenido la letra A. Una representación gráfica se puede ver en la Figura 1.
Nuestra etiqueta
letra que tenemos
pegada a la casilla no se puede mover a otra casilla, pero sí se puede asignar un nuevo contenido con una sentencia de asignación, tan simple como:
letra = 'B';Con el signo = estamos asignando un nuevo contenido a la casilla etiquetada por
letra: la letra B. ¿Donde va a parar la letra A que teníamos anteriormente? Podemos decir que se pierde para siempre, o que va la cielo de las letras A. Si tenemos el siguiente código, ¿qué tendremos en la variable
otra_letra almacenado al final?
char otra_letra = 'X';
otra_letra = 'Y';
otra_letra = 'Z';La repuesta es la letra Z, ya que es lo último que hemos "introducido" en la caja y lo que por tanto nos queda al final.
Las variables, además de almacenar datos, se pueden utilizar en operaciones. En el siguiente ejemplo tenemos dos casillas con números enteros (tipo
int) y almacenamos la suma en un tercero.
int a = 5;
int b = 2;
int c = a + b;¿Que contendrá la variable
c después de este trozo de código? La respuesta es que contendrá el número 7, que es la suma 5 + 2.
Punteros
Todo esto parece realmente sencillo ¿verdad? Bien, ahora vamos a pasar a los punteros, con los que mucha gente se atraganta, pero como veremos no tienen ningún misterio si se entiende bien el concepto.
Supongamos que las casillas, antes de que ningún programador decida etiquetarlas están numeradas según su posición en la memoria. Como están todas en fila esto resulta bastante sencillo. La primera tiene la dirección 0, la segunda la dirección 1, la tercera la dirección 2 y así sucesivamente. El sistema de asignación de etiquetas a las casillas es muy parecido al funcionamiento de una consigna. Nosotros le solicitamos al ordenador una casilla en la que poder meter nuestros datos; entonces el ordenador busca una casilla libre y nos entrega una ficha con el número de casilla, es decir, su dirección en la memoria. El lenguaje de programación nos permite asociar esta dirección a un nombre de variable, un alias, pero esto es sólo para facilitarnos la tarea de programación, en realidad, el ordenador sólo entiende de direcciones numéricas. Nosotros ahora podemos consultar en cualquier momento el contenido de nuestra casilla, o cambiar su contenido, ya que tenemos la reserva y la ficha con la dirección de la casilla.
Continuando con nuestro ejemplo de la consigna, imaginemos el siguiente ejemplo:
Nuestro jefe mensualmente nos deja la nómina en una casilla en la que nosotros podemos recogerla. El empleado de la consigna (el ordenador) cada vez le da una dirección de casilla distinta, según las que haya libres y ocupadas y no tenemos forma de predecir cual va a ser. Nosotros sólo podemos hablar con nuestro jefe una vez al año, por lo que no tenemos forma de saber en qué casilla está nuestra nómina cada mes. ¿Cómo se puede solucionar esto? De una forma bastante simple. La dirección de la casilla que contiene nuestra nómina es un dato, un número, y como tal puede ser almacenado en una casilla. Así que lo que acordamos con nuestro jefe es que yo tengo una casilla reservada que es siempre la misma y en la que él, mensualmente, puede dejar la dirección de la casilla donde está la nómina. De esta forma yo no tengo más que ir a mi casilla, recoger la ficha y entregársela al encargado para recoger mi nómina.
En esto mismo consiste el funcionamiento de los punteros. Un puntero es una casilla especial que en vez de contener datos directamente, contiene una dirección de alguna casilla que contiene datos. En la Figura 2 tenemos un ejemplo de un puntero (casilla azul) que contiene la dirección de una casilla tipo carácter que contiene la letra A. un puntero se declara de la siguiente forma:
char* direccion_letra;El asterisco se emplea para especificar que la variable es un puntero, y en este caso la palabra
char nos indica que la casilla apuntada contiene un carácter. Es muy importante no confundir. Un puntero sólo contiene la dirección y ocupa una casilla. Un puntero a una letra no contiene una letra, sino la dirección de la letra, un puntero a una fotografía contiene la dirección a la primera casilla de la fotografía, ya que una fotografía necesita muchas casillas para almacenarse. Un puntero a una cadena (un conjunto de caracteres, por ejemplo una frase) contiene la dirección de la primera casilla de la cadena, es decir, del primer carácter.
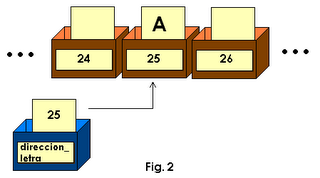
Como podemos ver, aún no hemos asignado ningún contenido a nuestro puntero. Vamos a crear una variable que contenga una letra y asignar a un puntero la dirección de la casilla que contiene la letra. Esto se hace mediante el operador &. El operador & delante de cualquier variable nos devuelve su dirección, en vez de su contenido.
char letra = 'A';
char* puntero_a_letra = &letra;Ahora tenemos una variable llamada
puntero_a_letra que contiene la dirección de la variable
letra. Sin intentásemos imprimir por pantalla el contenido de esta variable con printf(), nos imprimiría la dirección de la letra. Si lo que queremos es acceder al dato contenido en la dirección guardada, debemos anteponer el operador * delante del nombre del puntero. El operador * interpreta que la variable que hay a continuación es una dirección y nos devuelve el contenido de esa dirección. Hay que tener cuidado, ya que si lo anteponemos a una variable que no sea un puntero, puede interpretarla como si de una dirección se tratase y obtener resultados inesperados.
¿Puedes averiguar que hace el siguiente código? ¿Qué contendrán
letra1 y
letra2 al final del código?
char letra1 = 'A';
char letra2 = 'B';
char* puntero = &letra1;
letra1 = 'C';
letra2 = *puntero;
La respuesta es que ambas variables contendrán la letra C. En este caso estamos creando dos variables de tipo carácter y asignamos a la primera el dato 'A' y a la segunda 'B'. Después creamos una variable puntero a carácter (char*) y le introducimos la dirección de la casilla
letra1 (recordemos el operador &), más comúnmente dicho "hacer que apunte a
letra1". A continuación cambiamos el contenido de
letra1 por la letra C. Aunque hayamos cambiado su contenido, la dirección siempre será la misma. Finalmente cogemos el dato al que apunta
puntero con el operador * (de lo contrario devolvería el contenido de
puntero, es decir la dirección del dato) y lo metemos en
letra2, por lo que estamos metiendo en
letra2 el contenido de
letra1, es decir, la letra C.
Puede que esto os resulte confuso, así que os animo a repasar esta última parte y resolver estos sencillos ejercicios antes de pasar al último apartado.
Ejercicio 1
char letra1 = 'A';
char letra2 = 'B';
char* puntero = &letra1;
letra1 = 'C';
letra2 = *puntero;
¿Contenidos de
letra1 y
letra2 al final del código?
Respuesta
Pincha para mostrar
letra1 = 'C'
letra2 = 'C'
char letra1 = 'A';
char letra2 = 'B';
char* puntero = &letra1;
puntero = &letra2;
letra1 = *puntero;
¿Contenidos de
letra1 y
letra2 al final del código?
Respuesta
Pincha para mostrar
letra1 = 'B'
letra2 = 'B'
char letra1 = 'A';
char letra2 = 'B';
char* puntero1 = &letra1;
char* puntero2 = &letra2;
puntero1 = puntero2;
letra1 = 'C';
letra2 = 'D';
letra1 = *puntero1;
¿Contenidos de
letra1 y
letra2 al final del código? ¿A quien apuntan los punteros al final?
Respuesta
Pincha para mostrar
letra1 = 'D'
letra2 = 'D'
Ambos punteros apuntan a letra2
Teniendo el código.
char letra = 'A';
char* puntero = &letra;
Indicar cuales de la siguientes asignaciones son incorrectas y podrían producir errores:
A) letra = *puntero;
B) letra = &letra;
C) letra = &puntero;
D) puntero = *puntero;
E) puntero = *(&puntero);
F) puntero = *letra;
G) *puntero = letra;
H) &puntero = letra;
Respuesta
Pincha para mostrar
Son incorrectas B, C, D, F y H.
Operaciones con punteros
Ahora que ya hemos comprendido en qué consiste un puntero y como utilizarlo para tareas cotidianas.
Como dije anteriormente, un puntero es una dirección, y una dirección es un número. Por lo tanto podemos realizar operaciones matemáticas de cualquier tipo con ellos, aunque usualmente se utiliza la suma y la resta, y la multiplicación y división en casos muy específicos como el trabajo con matrices cuadradas, que no veremos aquí.
¿Qué significado tiene sumar 1 a un puntero? Como hemos dicho, todas las casillas de la memoria está numeradas consecutivamente. De esta forma, sumar 1 a la dirección contenida en un puntero es lo mismo que obtener la dirección de la siguiente casilla. Decrementar el puntero en uno significaría hacerle retroceder a la casilla anterior.
¿Tiene esto alguna utilidad? Pues sí. Como hemos visto antes, algunos datos necesitan más de una casilla para almacenarse, por lo que lo normal es guardar un puntero con la dirección de la primera casilla y acceder al resto mediante sumas a la dirección de ese puntero.
Veamos un ejemplo. Vamos a declarar una cadena. Una cadena es un conjunto de caracteres consecutivos, cada uno en una casilla de la memoria. En lenguaje C se emplea el carácter especial '\0' (barra invertida seguida de cero) para indicar el final de las cadenas, por lo que en principio no necesitamos saber su longitud; basta con recorrerla hasta encontrar el carácter especial que marca el final. Una cadena en C se declara así:
char* cadena = "Hola";Como vemos lo que en realidad estamos declarando es un puntero a
char. Efectivamente, la variable
cadena es, en realidad un puntero al primer carácter de la cadena, es decir, la letra H. Otro detalle a tener en cuenta es que las cadenas se declaran usando comillas dobles, y no simples como con los caracteres. Es muy importante no confundir la cadena "H" con el carácter 'H'. Para empezar, el uso del primero nos devuelve un puntero a esa cadena, mientras que el segundo nos devuelve el dato 'H' de tipo
char y no su puntero. En segundo lugar, la cadena "H" está en realidad ¡compuesta por dos caracteres! que son el propio carácter 'H', y el carácter especial que indica la final de la cadena '\0'.
Bien, veamos que podemos hacer con este puntero llamado
cadena que hemos creado. Si conocemos de antemano que la longitud de la cadena es 4, sin contar el carácter de final '\0', podríamos almacenar cada una de las letras en variables de carácter con las siguientes líneas:
char* cadena = "Hola";
char letra0 = *cadena;
char letra1 = *(cadena+1);
char letra2 = *(cadena+2);
char letra3 = *(cadena+3);
Nótese el uso de los paréntesis para sumar primero a la dirección y después extraer el dato contenido con el operador *. De no usar los paréntesis, la suma no se realizaría sobre la dirección contenida en
cadena, sino sobre cada uno de los datos. Dado que C trabaja con las letras como si de números se tratase, el resultado de sumar 1 a una letra es obtener la siguiente en la
tabla de caracteres ASCII, normalmente la siguiente letra del abecedario. El código anterior almacenaría el carácter 'H' en
letra0, 'o' en
letra1, 'l' en
letra2 y 'a' en
letra3. Sin embargo el siguiente código,
char* cadena = "Hola";
char letra0 = *cadena;
char letra1 = *cadena+1;
char letra2 = *cadena+2;
char letra3 = *cadena+3;
almacenaría 'H' en
letra0 ('H' + 0 = 'H'), 'I' en
letra1 ('H' + 1 = 'I'), 'J' en
letra2 ('H' + 2 = 'J') y 'K' en
letra3 ('H' + 3 = 'K').
También hay que tener cuidado al sumar o restar a punteros ya que se puede acceder a zonas de memoria libres y obtener resultados inesperados, o incluso un error del sistema operativo. Esto ocurriría en el caso anterior, si por ejemplo intentamos hacer:
char letra8 = *(cadena+8);Arrays
Un array es un vector de algún tipo de datos específicos, esto es, una reserva de un número determinado de casillas a las que accederemos con una única etiqueta. Por ejemplo, si quisiésemos guardar las temperaturas máximas de una población durante los doce meses del año podríamos declarar un array de números enteros (int) de longitud 12:
int temperaturas[12];
Esto nos reserva doce espacios en la memoria consecutivos de tipo entero. Podemos acceder a cada una de estas casillas usando el número entre corchetes, llamado índice del array. Es muy importante recordar que en lenguaje C el índice de los arrays siempre comienza por 0, y no por 1. Veamos como asignar valores a cada uno de los doce meses:
temperaturas[0]=15;
temperaturas[1]=18;
temperaturas[2]=22;
temperaturas[3]=23;
...
temperaturas[11]=12;
De momento esto es todo lo que necesitamos saber sobre los arrays. Lo importante es que, a efectos prácticos, un array es un puntero. es lo mismo acceder al primer elemento del array con
temperaturas[0] que con
*temperaturas, y como hemos visto que los elementos del array son consecutivos en la memoria, podemos acceder al segundo elemento del array con
temperaturas[1] o con
*(temperaturas+1). Igualmente podemos utilizar un puntero como si de un array se tratase. Si retomamos el ejemplo de la cadena "Hola" que puse en el apartado anterior:
char* cadena = "Hola";
char letra0 = *cadena;
char letra1 = *(cadena+1);
char letra2 = *(cadena+2);
char letra3 = *(cadena+3);
Otra forma de expresarlo podría haber sido:
char* cadena = "Hola";
char letra0 = cadena[0];
char letra1 = cadena[1];
char letra2 = cadena[2];
char letra3 = cadena[3];
Funciones: Paso por referencia y por valor
Una de las cosas que pueden parecer más descorcentantes cuando aprendemos le lenguaje C es por qué en determinadas llamadas a función es necesario anteponer el operador & a algunos parámetros, por ejemplo en la función
scanf(). Como vimos antes, el operador & sirve para utilizar la dirección de memoria de un dato, en vez del dato en sí mismo. ¿Qué diferencia puede haber entre pasar un dato y pasar la dirección del mismo?
Supongamos la siguiente función, que suma dos números enteros y devuelve el resultado:
int sumar(int valor1, int valor2) {
return valor1 + valor2;
}En esta función los parámetros se reciben
por valor, es decir, cuando la llamamos se reservan nuevas casillas y se copian los valores, por lo que cualquier cambio dentro de la función a
valor1 o
valor2 no tendría ningún efecto en el código llamante. Supongamos que modificamos la función anterior de la siguiente forma:
int sumar_cero(int valor1, int valor2) {
valor1 = 0;
valor2 = 0;
return valor1 + valor2;
}y la llamamos de la siguiente forma:
int num1 = 5;
int num2 = 3;
int resultado = sumar_cero(num1, num2);
Al finalizar esta ejecución la variable
resultado contendrá cero, ya que en el código interno de la función
sumar_cero() se convierten ambos sumandos a cero antes de sumarlos y devolver el valor. En cambio las variables
num1 y
num2 seguirán teniendo sus valores originales 5 y 3, ya que al pasarlas a la función estamos pasando una copia de sus valores, en unas nuevas casillas. Esto se puede ver en la Figura 3.
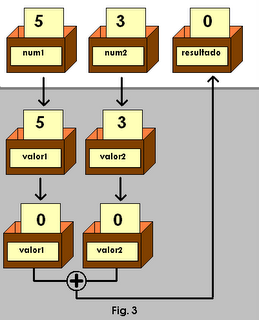
También podemos definir una función que reciba punteros como parámetros, o lo que es lo mismo, las direcciones de memoria que contienen. ¿Nos sirve de algo pasar una dirección de memoria a un dato, en vez de el dato en si? Cuando pasamos la dirección de memoria de una variable, la función tendrá acceso al contenido de la casilla original, y no sólo a una copia del dato, de forma que podrá realizar cambios en esa casilla, sí repercutirá en el código que llama a la función. A los parámetros que se pasan de esa forma se dice que son pasados
por referencia. Podríamos rescribir la función sumar anterior de la siguiente forma:
void sumar(int valor1, int valor2, int *resultado) {
*resultado = valor1 + valor2;
}En esta ocasión no estamos devolviendo el resultado, sino que lo estamos almacenando en el tercer parámetro de la función. Como la función recibe la dirección original donde se está almacenando el parámetro
resultado, sí tiene acceso a modificar el mismo. Así, el siguiente código almacena correctamente el resultado en la variable que enviemos como parámetro:
int valor1 = 5;
int valor2 = 3;
int resultado;
sumar (num1, num2, &resultado);
Como podemos ver, necesitamos utilizar el operador & para pasar la dirección de memoria de la variable, ya que de otro modo estaríamos pasando su valor. Si la variable resultado fuera un puntero esto no sería necesario, ya que su valor en sí mismo es la dirección de un dato:
int valor1 = 5;
int valor2 = 3;
int* resultado;
sumar (num1, num2, resultado);
Rizando en rizo
Todo lo visto hasta ahora han sido unos conceptos básicos sobre punteros. En realidad permiten hacer cosas mucho más complejas, pero podremos afrontarlas sin problemas si tenemos siempre muy presente que las casillas tipo puntero son iguales que todas las demás, con la diferencia de que el dato que almacenan es una dirección. Así mismo podríamos definir un puntero que apunte a casillas de tipo puntero que apunten a casillas que contienen caracteres:
char** puntero;Esto es la base para la construcción de matrices bidimiensionales o tridimiensionales, o los arrays de cadenas. Un array es un puntero, y una cadena también los es por lo tanto un array de cadenas es un puntero al primer elemento de una lista de punteros al primer carácter de una cadena.
También es bastante común el uso de punteros a
void. Un puntero a
void es un puntero genérico capaz de apuntar a cualquier casilla, independientemente del tipo que tenga. Se declara de la siguiente forma:
void* puntero;
Bueno, y eso es todo. Si tenéis alguna duda o corrección podéis dejarlo en los comentarios y estaré encantado de ayudaros en lo que pueda.












