Retomando el tema del otro día, que sirvió como introducción a los algoritmos genéticos, vamos a ver hoy por fin como funcionan realmente. Para ello resolveremos un problema muy sencillo pero muy ilustrativo del funcionamiento.
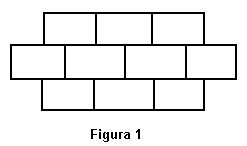
Tenemos una figura como la de la imagen de la derecha. Nuestro objetivo es colorearla usando únicamente tres colores (rojo, verde y azul) de forma que dos cuadrados contiguos no tengan el mismo color. Para esta figura en concreto existen 310 combinaciones posibles (aproximandamente 60 mil). Probar todas las combinaciones hasta encontrar con la mejor no supondría mucho reto a un ordenador de hoy en día, pero si en vez de tener 10 rectángulos la imagen estuviese compuesta por 200, el número de combinaciones posibles crecería hasta 3200, es decir, un 1 seguido de 95 ceros, lo cual haría que la exploración bruta de la mejor solución fuese impracticable.
Paso 1: Modelización matemática del problema
Como comentabamos el último día, un algoritmo genético se puede aplicar siempre las soluciones de un problema se puedan codificar numéricamente y siempre que dispongamos de un medio para decidir si una solución es mejor o peor que otra.
En el ejemplo del mapa podemos decir que una solución es mejor cuántas menos áreas del mismo color estén conectadas, así si todo el mapa fuera de un único color (el peor de los casos) el número de conexiones sería de 19, mientras que el óptimo buscado sería aquel con cero áreas conectadas compartiendo color. En principio no sabemos si esta configuración óptima existe, por lo que tras aplicar el algoritmo un número determinado de generaciones tendremos que quedarnos con la mejor solución encontrada.
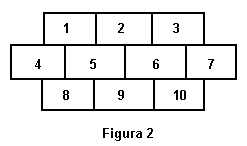
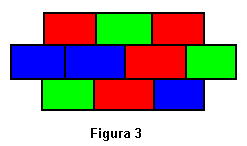
Para codificar las posibles soluciones primero numeraremos las celdas de la imagen, tal como se muestra en la figura 2. Representaremos la solución como la secuencia de los colores siguiendo ese orden. Por ejemplo, para la imagen de la figura 3 tendriamos la siguiente secuencia: RVRAARVVRA. Su puntuación sería 3, ya que exiten tres pares de celdas conectadas con el mismo color.
El siguiente paso es codificar esos tres colores en binario. El hecho de que sean tres, y no dos o cuatro plantea un problema adicional, ya que para etiquetar en binario los tres colores hacen falta por lo menos 2 bits, pero con 2 bits obtenemos etiquetas sin adjudicar. Por ejemplo podriamos codificar como:
R = 00
V = 01
A = 10
?? = 11
Pero aun nos queda la etiqueta 11 sin aplicar a ningún color. Al diseñar un algoritmo genético es deseable que esto no ocurra, ya que algunos miembros generados aleatoriamente, cruzados o mutados podrían resultar inválidos. Por supuesto existen varias soluciones pero a la hora de codificar en binario nuestros "individuos" conviene que sean válidos con cualquier combinación de bits, y que todas las cadenas de bits tengan la misma longitud. El segundo problema no aparece en nuestro caso.
Como este artículo pretende ser más explicativo que riguroso, optaré por continuar usando los dígitos R, V y A en vez de cadenas binarias.
Paso 2: Configuración del algoritmo
Existen una serie de parámetros de configuración del algoritmo genético. Estos parámetros pueden tener valores muy dispersos dependiendo de a qué problema nos enfrentemos. La única forma de conseguir los correctos la da la experiencia y el prueba y error.
Paso 3: Ejecución del algoritmo. ¡Manos a la obra!
En nuestro ejemplo vamos a comenzar con una población inicial de 6 individuos, que generaremos aleatoriamente: He aquí una primera población y la puntuación obtenida por cada uno de los individuos:
| Nº | Individuo | Puntuación |
|---|---|---|
| 1 | VAVRRRRRVA | 5 |
| 2 | VRARRVAVAA | 5 |
| 3 | VVRVARRRRA | 7 |
| 4 | RVVRAVAVVV | 8 |
| 5 | VVVRRVARRA | 9 |
| 6 | AAVAAAVARA | 11 |
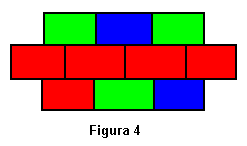
Examinando la primera población, generada aleatoriamente, observamos que los individuos no son muy buenos; en el mejor de los casos se obtiene una puntuación de 5, esto es, una figura con 5 regiones conectadas (Figura 4).
Selección
Una vez que tenemos la población inicial, debemos escoger los mejores individuos para cruzarlos. En nuestro caso cogeremos a los tres mejores, pero podría ser cualquier numero de ellos. Al igual que en otros parámetros, coger un número excesivo poducirá una siguiente generación más variada, pero a la que le costará más converger.
Cruce
Para hacer el cruce se unen por parejas, y se mezclan la mitad de los bits de un individuo con la mitad del otro. La forma de escoger los bits que aporta cada uno puede cambiar de un algoritmo a otro. Nosotros cogeremos las 5 primeras letras de un progenitor y las 5 siguientes del otro, pero podríamos haber cogido, por ejemplo, las que ocupan una posición par de uno y las que ocupan posición impar del otro. Como nos interesa que la siguiente generación esté compuesta también de seis individuos cruzaremos los 3 individuos todos con todos por la derecha y por la izquierda, de forma que obtengamos la siguiente generación con el mismo número de individuos que la anterior.
1 + 2 = VAVRR RRRVA + VRARR VAVAA = VAVRRVAVAA
1 + 3 = VAVRR RRRVA + VVRVA RRRRA = VAVRRRRRRA
2 + 1 = VRARR VAVAA + VAVRR RRRVA = VRARRRRRVA
2 + 3 = VRARR VAVAA + VVRVA RRRRA = VRARRRRRRA
3 + 1 = VVRVA RRRRA + VAVRR RRRVA = VVRVARRRVA
3 + 2 = VVRVA RRRRA + VRARR VAVAA = VVRVAVAVAA
En la Figura 5 se puede apreciar gráficamente el resultado del primer cruce.
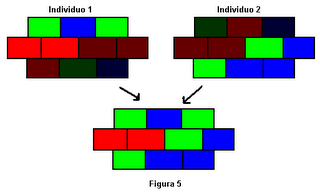
Mutación
Una vez hecho el cruce, se aplica la mutación. En nuestro caso vamos a mutar siempre dos individuos de cada generación. Los individuos mutados son escogidos al azar. Una vez que se tiene el individuo, se coge un gen (dígito binario o letra en nuestro caso) también al azar y se le cambia el valor. En el caso binario, cambiariamos un 0 por un 1, y viceversa. En nuestro ejemplo cambiaremos al azar el color correspondiente por uno de los otros dos. Los individuos mutados en esta nueva generación elegidos al azar han sido el 1º y el 4º:
VAVRRVAVAA --> (mutación) --> VVVRRVAVAA
VRARRRRRRA --> (mutación) --> VRARRRRRVA
Después de esto se junta de nuevo a los individuos mutados con la nueva generación y ya tenemos la siguiente generación, cuyas puntuaciones son las siguientes:
| Nº | Individuo | Puntuación |
|---|---|---|
| 1 | VVRVARRRVA | 5 |
| 2 | VVVRRVAVAA | 7 |
| 3 | VRARRRRRVA | 7 |
| 4 | VRARRRRRVA | 7 |
| 5 | VVRVAVAVAA | 7 |
| 6 | VAVRRRRRRA | 8 |
Vaya, parece que no hemos avanzado mucho. La selección, al igual que el la vida real, es un proceso largo y gradual, y es muy poco probable que una generación sea automáticamente superior a la anterior. Veremos que en algunas ocasiones las generaciones posteriores son peores que las anteriores, pero a la larga es cuando se obtienen resultados.
Una vez preparada la nueva generación, repetiremos de nuevo los pasos selección, cruce y mutación, para obtener la tercera generación, y así sucesivamente, hasta encontrar el individuo óptimo (si sabemos cual es) o hasta que creamos que el algoritmo ha convergido a una buena solución.
Paso 3: Resultados
Si seguimos ejecutando el algoritmo anterior, generación tras generación, finalmente llegaremos al mejor individuo en la generación número 26. Esta es la población de dicha generación:
| Nº | Individuo | Puntuación |
|---|---|---|
| 1 | VRARAVRVRA | 0 |
| 2 | VRA;RAVRRVA | 1 |
| 3 | VRARAVRRVA | 1 |
| 4 | VRARAVRRRA | 1 |
| 5 | VRARAVRRRA | 1 |
| 6 | VRARAVRRVA | 1 |
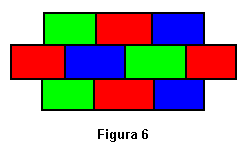
Como se puede observar, no sólo tenemos un individuo que cumple con nuestras espectativas, sino que la población en su conjunto ha mejorado notablemente. Además, los individuos son muy parecidos unos con otros, el algoritmo converge. En la Figura 6, se muestra al individuo de puntuación 0 que efectivamente no tiene todas las celdas contiguas del mismo color.
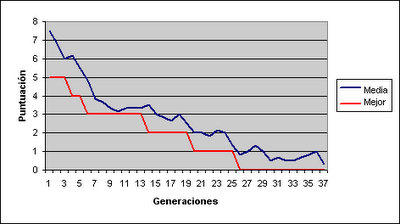
¿Qué ha ocurrido en el transcurso del resto de generaciones? Sería muy largo escribir aquí una a una todas las generaciones y los pasos seguidos, pero podemos hacernos una idea con la gráfica siguiente, en la que se muestra la puntuación del mejor individuo de cada generación y la puntuación media de los individuos de cada generación.
Si a alguien le interesa, para el experimento he desarrollado un programa en Java como implementación del algoritmo genético. Lo colgaré por aquí en los próximos días.
6 comentarios:
muy interesante el blog, felicidades
lo unico que no me a gustado es q eres un poco feillo ;)
Uff, que rarillo es el usuario anónimo ese de arriba eehh xD.
Espero respondas antes del 29 de oct del 2008, solo dime cual seria la funcion de adaptacion de este caso para programarlo en java, es una tarea que me urge a la de ya, si tienes por ahi el código que mejor, publicalo o pasalo no?, gracias....
Hola juan manuel,
El programa lo perdí hace tiempo. Cosas que pasan a los discos duros cuando no haces copia de seguridad. De cualquier forma más o menos recuerdo como iba.
En este caso en concreto, tenía un Array de parejas de celdas conectadas (por sus indices). Puedes hacerte una clase que contenga los dos indices o usar una cadena como "X,Y" y hacerlo por tratamiento de cadenas. Creo que yo opté por esta última opción (por rapidez).
La cadenas de emparejados para esta distribución del mapa son:
(1,2) (1,4)
(2,3) (2,5) (2,6)
(3,6) (3,7)
(4,5) (4,8)
(5,6) (5,9)
(6,7) (6,10)
(8,9)
(9,10)
Podrías hacer un algoritmo que te sacase las parejas para cualquier mapa arbitrario, pero te aseguro que no es una tarea sencilla.
Entonces la función de adaptación consiste en comprobar cada pareja y si son del mismo color sumarle 1 a un acumulador, que será el resultado final. Si quieres normalizar el resultado entre 0 y 1 simplemente divídelo entre el número de parejas, 16 en nuestro caso.
Espero que te haya sido de ayuda.
Hola que tan!!
Soy estudiante y me interesa mucho exponer el tema..Solo un favor, tendrían el código en java que mencionas en la publicación?.
Si lo tienes puedes ponerlo al publico por favor. Gracias!!
Publicar un comentario